ICASP 13 - Information Theory and Machine Learning for data-driven Risk Analysis

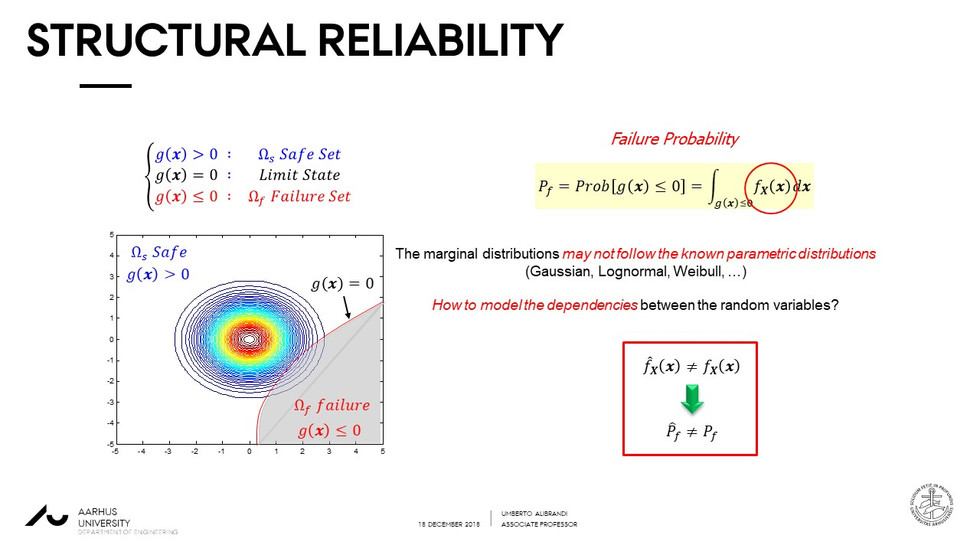
In ICASP13 We have presented the paper "Distribution with Independent Components for Uncertainty Quantification and Structural Reliability Analysis" by U. Alibrandi & Khalid M. Mosalam

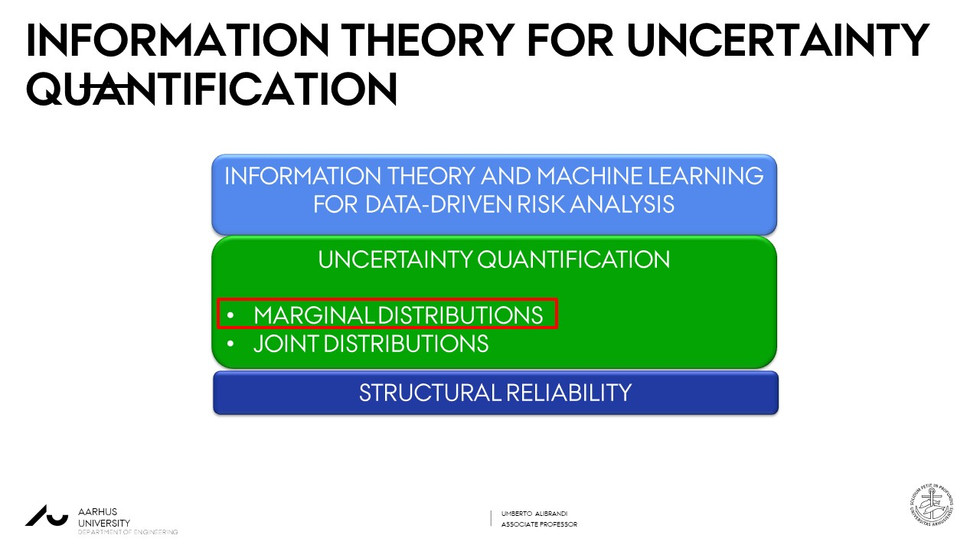
In this paper we show a novel framework based on the Information Theory, Machine Learning and Independent Component analysis for Uncertainty Quantification and Structural Reliability Analysis.

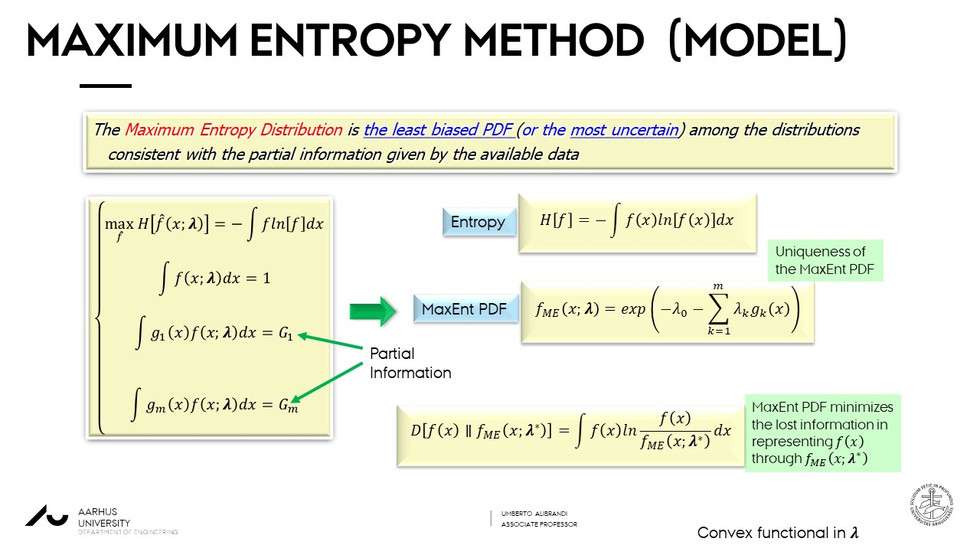
At first, we note that the optimal probabilistic model may be determined through minimum relative entropy and the theory of statistical learning.

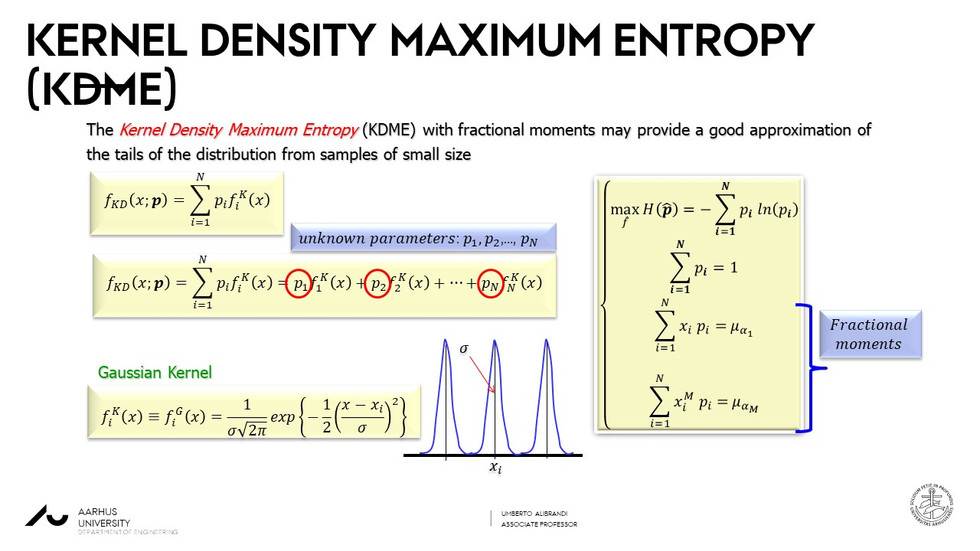
Then, we note that methods based on the maximum entropy may perform well for the evaluation of the marginal distributions, including the tails, from small samples of data.

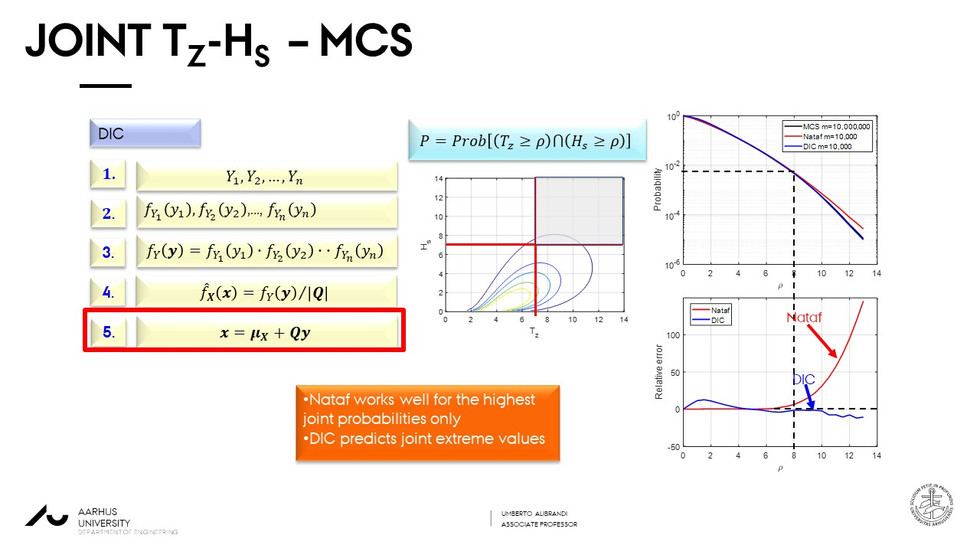
To determine the joint distribution of the basic random variables we introduce the multivariate probabilistic model of Distributions with Independent Components (DIC).

It has the same computational simplicity of Nataf, but it is more accurate, since it does not pursue any assumption about the tail dependency. The proposed framework is applied to determine the joint distribution of wave height and period of wave data.